Davide Gessa @dakk

Davide Gessa @dakk

I’m Davide Gessa, a software developer, computer scientist and sailor.

Solving Sudoku Puzzles on a Quantum Computer

Today, I’m going to show you how to use Qlasskit to create a quantum circuit able to search for Sudoku puzzle solutions.

Qlasskit, is an open-source Python library developed with the support of a Unitary Fund microgrant, addresses this challenge head-on by allowing direct translation of standard Python code into invertible quantum circuits without any modification to the original code.

Using qlasskit for this use case, will allow us to write and execute a quantum circuit, writing only python code without any quantum related primitives.

Since current quantum computers are very limited machines, we cannot solve a real 9x9 sudoku puzzle; our toy examples uses a 2x2 matrix where a valid solution is when in every row and every column there are no repeated values (0 or 1). We encode these xor-ing the values for each row and column.

Since we want a specific solution, we add a constraint constr: we want the [0][0] element to be True.

from qlasskit import qlassf, Qmatrix
from qlasskit.algorithms import Grover


@qlassf
def sudoku_check(m: Qmatrix[bool, 2, 2]) -> bool:
    constr = m[0][0]
    sub0 = m[0][0] ^ m[0][1]
    sub1 = m[1][0] ^ m[1][1]
    sub2 = m[0][0] ^ m[1][0]
    sub3 = m[0][1] ^ m[1][1]
    return sub0 and sub1 and sub2 and sub3 and constr

Now that we have an oracle, we can instantiate the Grover search algorithm:

q_algo = Grover(sudoku_check)

Then we use our prefered framework and simulator for sampling the result; this is an example using qiskit with aer_simulator.

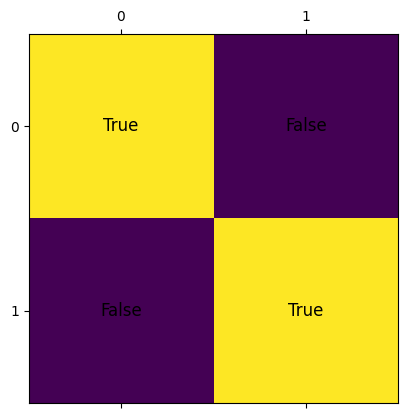
We obtain that the solution for this puzzle is the matrix [[True, False], [False, True]].

from qiskit import Aer, QuantumCircuit, transpile
from qiskit.visualization import plot_histogram

qc = q_algo.export("qiskit")
qc.measure_all()
simulator = Aer.get_backend("aer_simulator")
circ = transpile(qc, simulator)
result = simulator.run(circ).result()
counts = result.get_counts(circ)

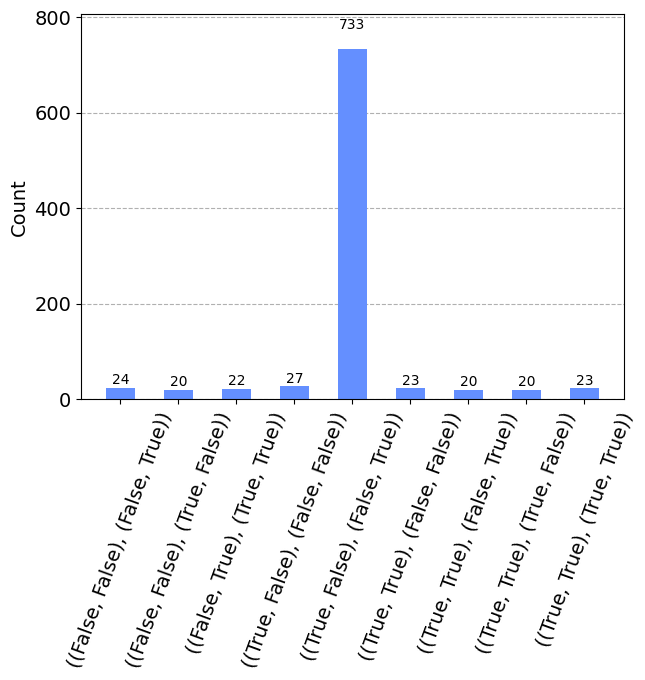
counts_readable = q_algo.decode_counts(counts, discard_lower=20)

plot_histogram(counts_readable)

We can exploit matplotlib for drawing the result sudoku matrix as follows:

import matplotlib.pyplot as plt

def draw_matrix(matrix):
    fig, ax = plt.subplots()
    ax.matshow(matrix, cmap='viridis')

    for i in range(len(matrix)):
        for j in range(len(matrix[0])):
            ax.text(j, i, str(matrix[i][j]), va='center', ha='center', fontsize=12, color='black')

    plt.show()
    
m_res = list(filter(lambda x: x[1] > 500, counts_readable.items()))[0][0]
draw_matrix(m_res)

We can create a more realistic sudoku game using numbers instead of booleans, but the resources required will scale exponentially. In the following code snippets, we recreate sudoku_check using Qint2 and a 4x4 matrix. The sum of each column and row must be equal to 6 (3+2+1+0). As we can see, the resulting circuit of the checker requires more than 100 qubits, way above our simulation capabilities.

from qlasskit import Qint2, Qint4

@qlassf
def sudoku_check(m: Qmatrix[Qint2, 4, 4]) -> bool:
    res = True

    # Constraints
    res = (m[0][2] == 3) and (m[0][0] == 1)

    # Check every row and column
    for i in range(4):
        c = (Qint4(0) + m[i][0] + m[i][1] + m[i][2] + m[i][3]) == 6
        r = (Qint4(0) + m[0][i] + m[1][i] + m[2][i] + m[3][i]) == 6
        res = res and c and r

    return res

print(sudoku_check.circuit())

QCircuit<sudoku_check>(1309 gates, 178 qubits)

Useful Links:

2024

DQPU, the decentralized quantum simulator

2 minute read

During my Quantum Computing journey, I often needed to simulate some quantum circuits; sometimes they are small, but some other times they are bigger enough ...

The Time I Built a Probabilistic Computer

6 minute read

In early 2023, I embarked on a journey to explore the field of probabilistic computing. This endeavor culminated in the construction of a hardware prototype,...

Back to Top ↑

2023

Expanding the Commodore 64 Quantum Emulator

1 minute read

In a recent article I wrote, “Quantum Computing on a Commodore 64 in 200 Lines of BASIC”, published both on Medium and Hackaday.com, shows a two-qubit quantu...

Back to Top ↑

2020

OCaml and Quantum Computing

1 minute read

Qiskit is a python SDK developed by IBM and allows everyone to create quantum circuits, simulate them locally and also run the quantum circuit on a real quan...

Yallo, a new Tezos language

2 minute read

As someone noticed from the previous post, last weeks I started to write a new programming language for Tezos smart contracts. This project was initially int...

King of Tezos: a smart-ponzi on Tezos

2 minute read

While writing a new programming language, it is often useful to write some real use-cases to test the syntax, the language expressiveness and the code cleann...

Favorite dev quote

less than 1 minute read

Documentation is like sex: when it is good, it is very, very good; and when it is bad, it is better than nothing

New blog

less than 1 minute read

This is my new blog, based on jekyll. I’ll soon import old posts from my old blog.

Back to Top ↑

2016

Contractvm: decentralized applications on Bitcoin

less than 1 minute read

Contractvm is a general-purpose decentralized framework based on blockchain. The framework allows to implement arbitrary decentralized applications in an eas...

Back to Top ↑

2015

Dices provably fair - Nonce overflow vulnerability

less than 1 minute read

Most of bitcoin dice software use a system to prove the fair play of the server for each bet. Most of them implement this mechanism using two seed (server se...

Back to Top ↑

2014

Apache2: redirect different domains to subfolder

less than 1 minute read

In the aim to merge two of my server on digitalocean, today I tried to write a mod_rewrite rule to redirect a secondary domain to a subfolder. After one hour...

Back to Top ↑

2013

MineML: F# miner

less than 1 minute read

MineML is a multithread CPU based bitcoin miner written in F#. At the moment it’s a slow implementation, but the class structure offers the possibility to im...

Back to Top ↑